第7回#2 学生が何を感じるかに思いを馳せた教材作成を目指して(中)
KETpicは LaTeX文書に数式処理(リスト処理)ソフトで作成した図を挿入することができるマクロパッケージであり、最近は動的幾何ソフトウェア Cinderellaとの連携も行われている。KETpicの開発経緯と、それを活用した教材作成に対する思いを、開発者である東邦大学訪問教授、高遠節夫さんにお聞きした。
(インタビュアー:CIEC会誌編集長 中村泰之)
※ Special第7回は、CIEC会誌『コンピュータ&エデュケーション』(Vol.39)の巻頭INTERVIEW(pp.3-10)を、3号(上・中・下)に分けてお送りします。今回はその「中」です。
教育的に適切な図とは -俳句の世界に通じるもの-
今まで、最初の教科書との関わりから、KETpicが生まれるまでの話を伺いましたが、根底にあるのは、きれいな図を描きたいということですか。
きれいな絵というより、教育的に適切な絵と言った方がいいと思いますね。数学の教材として使う絵というのは、俳句の世界に通じるんです。例えば Mapleとか Mathematicaで非常にきれいな絵が出ますよね。こういう色のついた、あるいはワイヤーフレームで描くときれいにできるでしょ。ところがもしその絵を、プリントして学生全員に配ったとしても、彼らは書き込みができないんですよ。書き込むスペースが無いから。
数学で大事なのは学生自身が作業をすること
数学で大事なのはやっぱり彼らがアクティブというか、彼ら自身が作業することです。そのためにはできる限り書き込みの場所を空けておかなくちゃいけない。そのためにどうするかというと、本当に必要最低限のものに絞って、ただそれでもって、どんな立体かわからなくなったらアウトなんだけど、そうじゃなくて、立体として認識できて、空きスペースをつけてあげる。そのための工夫というのがやっぱり今回の KETpicじゃないかと思うんです。
俳句の、五七五の 17文字だけで表すことに通じるということですね。
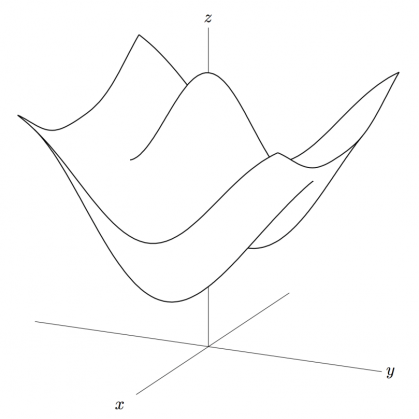
そうそう、あの中に収め込んですべての世界を描いていく。だから俳句の世界。ちょっとお見せしてもいいですか。この絵を見てもどんな絵かわかるでしょ。だいたいどんな立体かっていうのが。
山のてっぺんみたいなものがあって、こっちが長くなって、底と谷があるみたいな感じ。これは線としてはものすごく少ないんですよ。だけど十分立体的に見える。こうしておくと、授業のときに書き込みができる。それが俳句の世界だと思うんです。
実は KETpicの最初の頃は平面のバージョンしかなかったけれど、次にはやっぱり空間も入れていかなくちゃならないときに、ワイヤーフレームの方法は使いたくなかった。始めから。だってワイヤーフレームはきれいかもしれないけれどあまりにも線が密になっちゃうから。中に書き込みができなくなっちゃうんですよ。だからそれをなんとか、どうしようかなというのが次の年くらいの課題だったんですけど、その中でこの輪郭を捕まえてくると、この山の輪郭をどこで止めるかが課題でした。
ここの山の端っこですね。
そうそう。富士山なんかの絵を子供でも描くじゃない。そのときに縁はすっとは流さないでしょ。どこかで止めるじゃないですか。でもどこで止めたら自然に、自然の山として見えるかというのを、 KETpicではちゃんと数学的に計算して求めているんです。そこがポイントじゃないかなと。これをちゃんと止めることによって山に見えてくる。画家、特に日本画家というのはわかっていると思いますよ。どうなっているかというと、ここが面が回り込んでいくところなんですよね。それを平面に落とした時にカスプという、ここでとんがってくるという状態になるんですよ。
なるほど。そういう計算というのは数式処理の力を借りて行うのですね。
ただ今のところの欠点は、計算時間がかかりすぎることです。これ 1枚、2,3分かかるんですよね。だからやっぱり、外部プログラム、関数を呼ぶことができるようになれば、それが 100分の 1くらいに、少なくても 1桁は間違いなく違ってくるので、そうなればいいと思います。
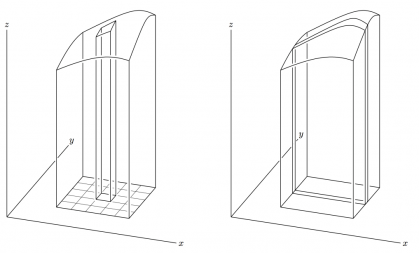
それから、この図はちゃんとスケルトンかかっているんですよね。スケルトンというのは、この線がちゃんと向こうの線を消しているでしょ。これで立体感を出しているんですよ。
わかりますよね。
積分の例だと、こんなのは結構いいでしょ。スケルトンというのは透けているのでね、かなり立体感がある。xとか Δxを書かせたり、といった作業を入れるにはこっちの方がいいんですよ。
重要なのはきれいな図というよりは、教育のために適切な図であるということがよくわかりました。
そうですね。そのためにはできるだけ余分な線は消すと。
そして、できるだけ学生に書き込ませる。
そう、最小限の線にして学生ができるだけ自分でいろんなことができる、書き込みができる。でも、同時にやっぱり美しいということも学生にとっても大切なんです。喜ぶんです。マントみたいだとか。これに目を描いたりするんですよ。今では漫画もかなりリアルに描いたりいろいろつけたりするけど、初期の漫画ってこんなもんでしょ。あのころはインクも紙も高くて高度な印刷はできなかったから、単色で塗ったりして。でもそれでも十分で、漫画の原点じゃないですか。
図を見る学生の視線に着目して
おばけの Q太郎はこういう感じですよね。学生がこの絵を見てすごく喜んだっておっしゃいましたけど、たしか図を見せながら脳波を測定することもなさっていると伺いましたが。
それに関しては、発展途上というか、まだきちんとやってないんですが、その一つとして、アイマークを使って視点がどこに行くかについて調べる実験があります。スケルトンで描いた正八面体を見せて、彼らの視点がどこに行くかを測定すると、これ全体を見ているようなんだけど、実はこのポイントに止まるんですよ。さらに式があると、式のところと行ったり来たりする。ただそれがあまりにも複雑な式だとそこで止まってしまって、意味が分からなくてなかなかこっちに戻ってこないということもあるんですけど。一昨年やった実験ではそんなところが出てきている。ただまだ定量化できていなくて、それをどういうふうにやって客観的に評価していくかということはまだできていないんですけどね。何か面白そうなものが出そうな感じですね。
図形を見て、それが数式とどんな関連があるのかという思考を学生の視点に着目して解析するということですね。
目の動きでもかなりわかります。
その時にはこういった線画を使う方が、適切であると。
たぶんね。その時は両方見せたんですよ。Mapleで作って色をつけたものと。Mapleだとバーッと全体を見るけど、視点が止まらないの。だからたぶん全体はパッとつかめているようなんだけど、細かいとこに行かない。一度見て「あぁわかっちゃった」っていう感じ。
要するに線画と、きれいな図との違いで、線画の方が図の特徴を数式と照らし合わせやすいということですか。
そうです、頭がカチカチ動いている感じ。最近はね、私じゃないんだけど、木更津のほうで、脳波をやってる人がやってみたら、やっぱりものを考える、図で考えると、この辺りが発色してくるんですよ。やっぱり頭が働いているというか、温度が高くなっているというのが見えています。
私は物理の授業を担当しているんですけど、以前、運動を視覚化させるようなシミュレーションの教材を作成してそれを学生に見せると、学生はわかった気にはなるんですが、果たしてそれで理解できているのか、ということが疑問だったんですね。物理現象と数式とを行き来するというところが難しくて。
そうなんですよね。シミュレーションに近いかもしれないけど、動的な教材ってあるじゃないですか。Mapleとか Mathematicaとかのアニメーションとか。その時に、1回目は喜ぶのね。流して1回目はね。それは波が動いているからなんだけど、波の式とは結びつかないの。で、2回か3回やってくると飽きて寝ちゃったりとかするんです。
その時にそれを補うものとして、先生たちがやられているのがパラパラ漫画ですね。
そうです。あれはいいと思う。可能性あると思うんですよ。あれ自体を配っておくこともできる。 PDFですからね、そのまま持ち帰って見てもらうこともできるし。授業で見たものと同じ図が手元に1枚とか2枚とかここにあると、やっぱり違うんじゃないかなと思いますね。
KETpicから KETCindyへ
これまでお話をお聞きしていると、KETpicというものを使って教材、あるいは教科書の図を作成するというのは、学生が使ったり見たりするもので、学生のためということに力点というか視点が置かれているように思うんですけど、最近は Cinderellaという動的幾何ソフトウェアを使った KETCindyへの取り組みがありますが、これはむしろ作成者側の負担を軽減するというねらいでしょうか。

KeTpic with Cinderella
そう、負担軽減もありますけど、可能性としては Cinderellaをそのまま学生の方に渡して、そのうえで彼らが操作して、その後に同じ資料を配布したりだとか、いろんな組み立てができると思います。教材というのは一つの方法だけではなく、併用しながら、どういうふうに組み合わせるとより効果的かということを考えていかなくちゃいけないと思います。たとえば、Cinderellaの可能性、学生に対する可能性としては、操作しながら、自分がいいと思った図形、この中に何らかの性質がありそうなものが見つかったとするじゃないですか、そうしたらそれを PDFで文書として作成できるので、これいいなと思ったらボタンを押して出して、それをプリントアウトしてもいいし、まぁ最近だったら PDFに直に描けるから、そこにいろんなコメントを、手書きで書いてもらったっていい。
それはコンピュータ上でということですか?
コンピュータ上で書いてもいいし、彼ら自身が印刷をして、この絵のここがこうだと自分で気が付いたことを書き込んでいく。手書きでいいんですよ。だからそういう使い方が僕はあると思うんですね。
教材の自作に向けて
今伺って共通しているのは、学生にいかに手を動かして考えさせるかということが重要であるということですね。でも、教材を教員が準備するというのは正直大変な部分もあると思うんですけれども、その辺の負担の軽減というか、あるいはむしろ啓蒙を狙って今全国でワークショップを開催されているということなんでしょうか。
単にあるものを持ってくるんじゃなくて、やっぱり自分でいろんな教材を作ってほしいんですね。で、その時には TeXは大きなネックではなくて、やっぱり図なんです。数学の教材で図が無いということはありえないから。概念図でもいいですよ、何かないと授業が成り立たない。TeXを使う中で慣れてくれば、特に最近の Cinderellaを利用すれば楽になった気がする。例えば、これは統計の授業で使う教材で、データを与えて、データは少ないんだけど、散布図と相関係数を計算してみようというような問題なんです。
理学部の2年生ですか。
環境系の学科ですけどね。そこで初めて統計をやるんだけど、今までの問題だったらこれ(グラフ用紙)がいっしょに描かれてない。ところが課題用紙にくっつけておくと、全然書き方違うの。
グラフ用紙を別に用意してやるというのとは違うのですか。
それでもいい。普通はそうやります。だけど、1枚の紙にまとめておくことが大事なんです。グラフ用紙に描くとどっかにいっちゃうしね。だから必要な方眼紙をつけておけばいいじゃないですか。大変そうに思うけど、作れば作るほど楽になる、特に TeXの場合は作れば作るほど自動化してくれるというところはあると思います。
今までのお話の中で、いかにいいものをつくるかということは、「必要は発明の母」という言葉もありますけど、学生達にいかに良い教育を受けさせたいか、そのためにはどういった教材を用意するべきかを突き詰めていかれているという印象を受けました。
その通りです。
それを突き詰めていけば KETpicを使うということが一つの解になるんじゃないかということですね。
このマークシート式の問題も、マーク部分もそうだけれども、図もちゃんと入れられるんです。後でこのマーク欄を集計する。このマークシートも全部 KETpicで作りました。
これをスキャンして読み込ませて、集計するのですね。
そうです。最初は市販のマークシートでやろうと考えたんです。でも市販のものはどうも合わないの。やっぱり数式も入れなくちゃいけないし、それとこれとを組み合わせたいとなってくる。で、これを週に3回くらいやったんですよ。1回やると集計結果をバーッと出して、また次のものを配ったりして。
こういうものも慣れてくれば、簡単にできるようになるのですね。
問題ないです。形は決まってくるんですよ。ここはもう決めておくとか。ここの欄は決めておいて、あとは横にいったら番号だけふっておくとかね。絵は入れる場合と入れない場合がありますけど。
この続きは「第7回#3 学生が何を感じるかに思いを馳せた教材作成を目指して(下)」をご覧ください。